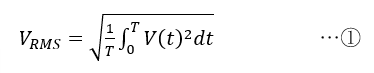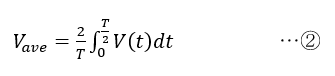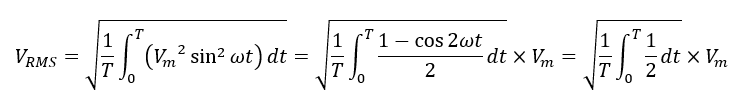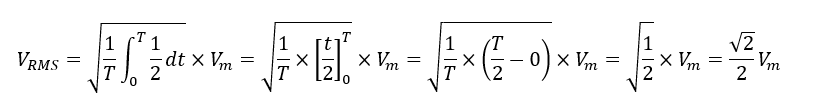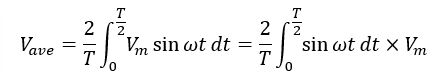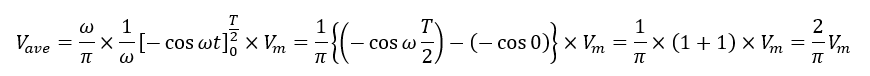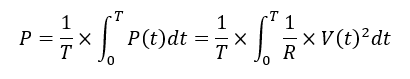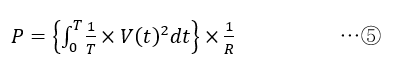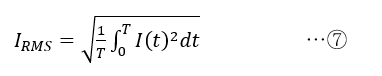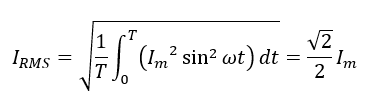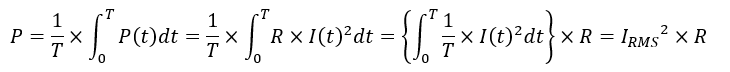[正解]

　(エ)　

 

[解説]

　交流電圧の実効値と，負荷に供給できる電力に関する問題です．

 

●交流電圧を表す3つの方法

　交流電源の電圧は，振幅が±Vm，角速度がωの正弦波

V(t)＝V_m sinωt

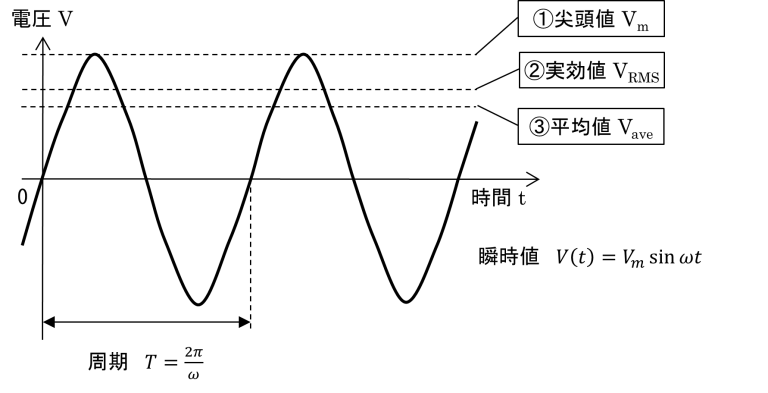
で表されます．このV(t)は時間とともに常に変化し続ける量ですが，1個の値で表現する方法がいくつかあります．図1に示す①尖頭値（ゼロ-ピーク値），②実効値（Effective Value），③平均値（Average Value）がよく使われています．

 

図1　交流電圧を表す3つの方法

 

なお，時間t＝0のときωt＝0，t＝Tのときωt＝2πなので，周期Tは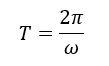

 

となっています．
　実効値については設問の文でも説明していますが，瞬時値の2乗（Square）を求め，1周期にわたって積分してTで割ることによって平均化（Mean）し，平方根（Root）を求めたものです．Root Mean Squareを略してRMS値とも呼びます．実効値の式は，

のようになります．

　したがって，解答群のア「交流電圧の実効値とは，瞬時電圧の二乗和を平均したものの平方根に相当する．」は正しい文章です．

　一方，平均値は瞬時値をそのまま平均化したものです．ただし，正弦波は1周期の前半で正の値，後半で負の値をとり，平均化すると0になります．そこで，通常は前半の1/2周期を積分してT/2で割って平均化します．したがって，平均値の式は，

のようになります．

 

●正弦波交流電圧の実効値と平均値の大小関係

　①式にV(t)＝V_msinωtを代入すれば，正弦波交流電圧の実効値を計算できます．
　まず，実効値ではV(t)²＝V_m²sin²ωtを計算する必要があります．三角関数の倍角公式を利用すれば，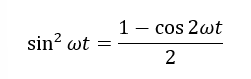

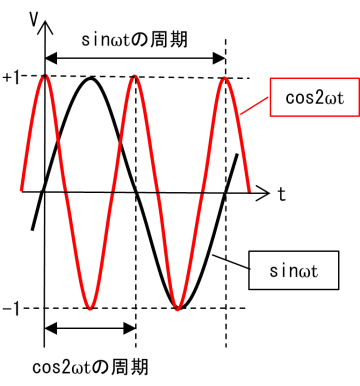
と書けます．図2にグラフを示します．

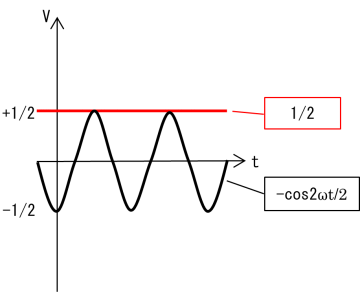
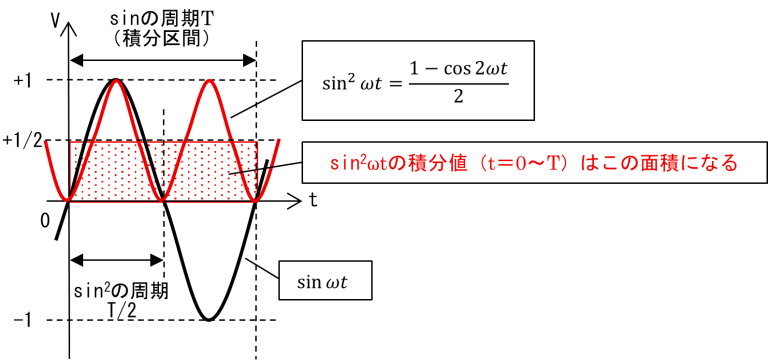
　cos2ωtはsinωtの1/2の周期をもつ三角関数で，－cos2ωtはその正負を反転したものです（図2(a)）．その振幅を1/2にした－cos2ωt/2を定数1/2に加えたものがsin²⁡ωt=(1-cos⁡2ωt)/2 となります（(図2(b)）．ここで，－cos2ωt/2の部分を周期Tにわたって積分すれば正と負が打ち消しあって0になるので，sin²⁡ωt=(1-cos⁡2ωt)/2の積分は定数1/2の部分だけを積分していることになります（図2(c)）．

 

図2　sin²ωtのグラフ

(a) sinωtとcos2ωt

(b) 1/2と－cos2ωt/2

(c) sinωtとcos2ωt

 

したがって，実効値は

となり，定数1/2を0からTまで積分すれば，

と求められます．√2/2≒0.707なので，実効値V_RMSは尖頭値V_mの約0.7倍です．

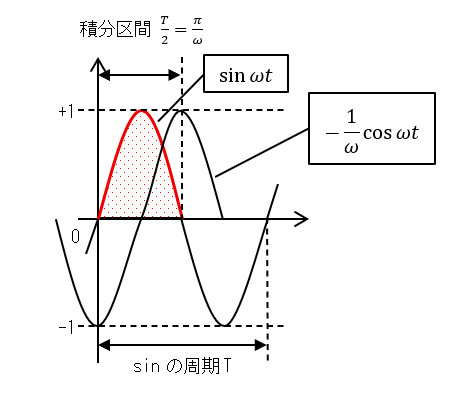
　同様に，こんどは②式にV(t)＝V_msinωtを代入すれば，正弦波交流電圧の平均値を計算できます．sinωtおよび積分区間のグラフは図3のようになります．

図3　sinωtのグラフ

 

したがって，平均値は

となります．

　ここで，sinωtの積分は－(1/ω) cosωt，積分区間はT/2＝π/ωなので，

となります．2/π≒0.637なので，平均値V_aveは尖頭値V_mの約0.64倍と言えます．

　したがって，実効値V_RMS≒0.71[V_m]は平均値V_ave≒0.64[V_m]より常に大きく，解答群のイ「正弦波交流の場合，電圧の実効値は電圧の平均値より大きい．」は正しい文章です．

 

●実効値と電力の関係

　一般的な商用電源の電圧は実効値が100Vになっています．これは，設問の文でも簡単に説明しているように，負荷抵抗で消費する電力が，実効値100Vと直流100Vで同じになるからです．なお，交流では電力も変化し続ける値なので，ここでは平均電力を考えています．

●直流電圧と電力の関係

 

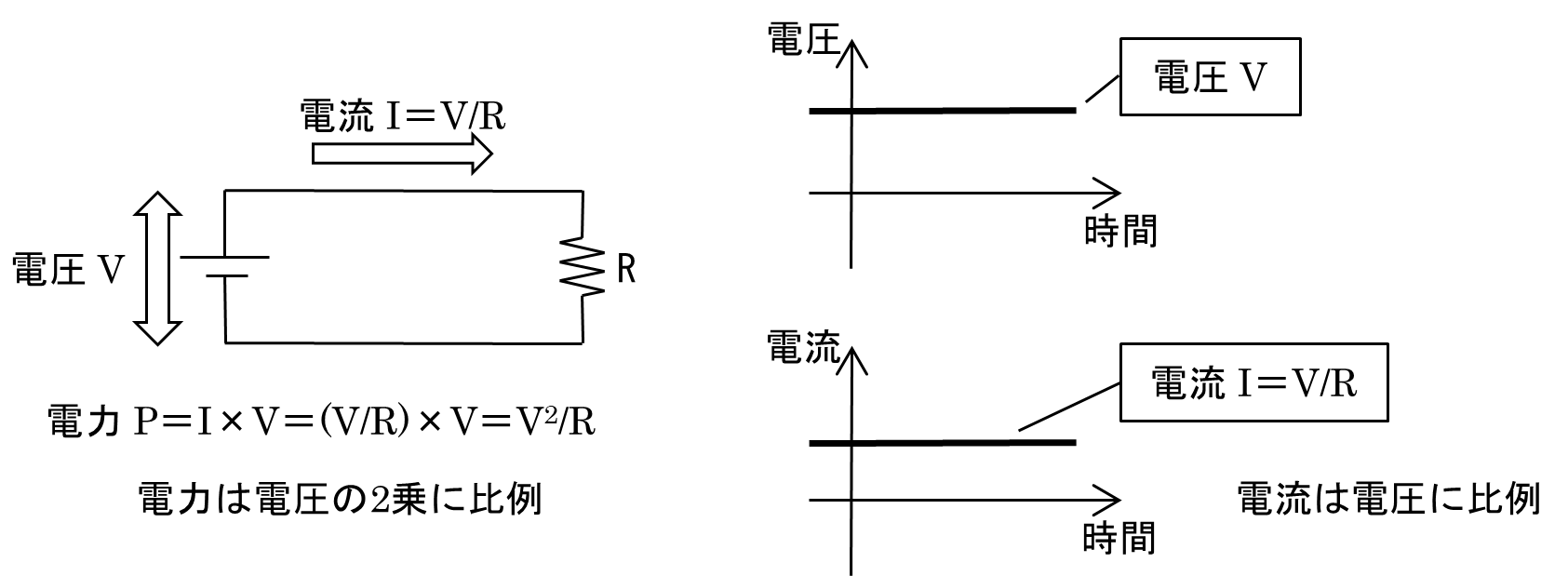
　図4(a)のように負荷抵抗Rに直流電圧Vをかけると，RにはVに比例した電流I＝V/Rが流れます（オームの法則）．抵抗が消費する電力Pは電流Iと電圧Vの積であり（ワットの法則），

P＝I×V＝V²/R　　　　　…③

です．すなわち，電力は電圧の2乗に比例します．

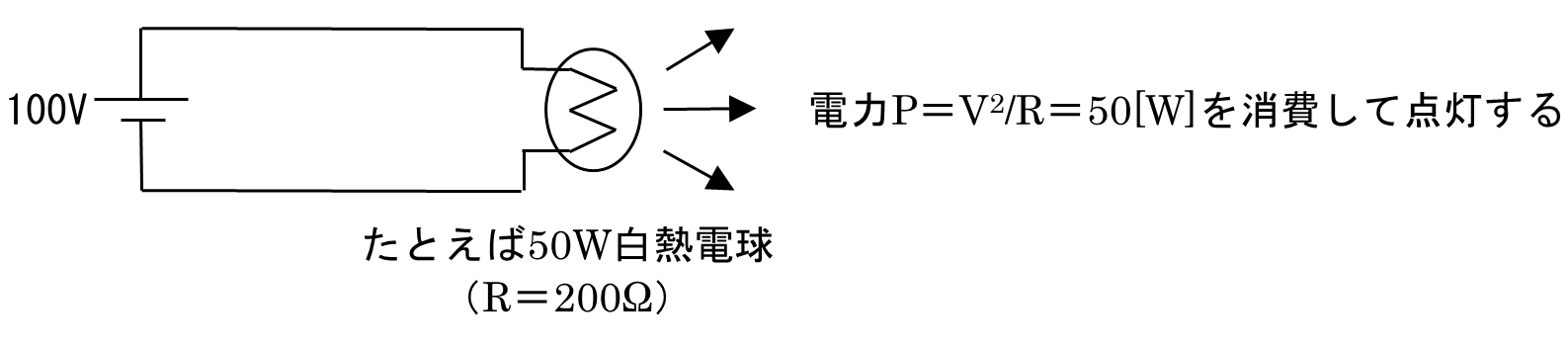
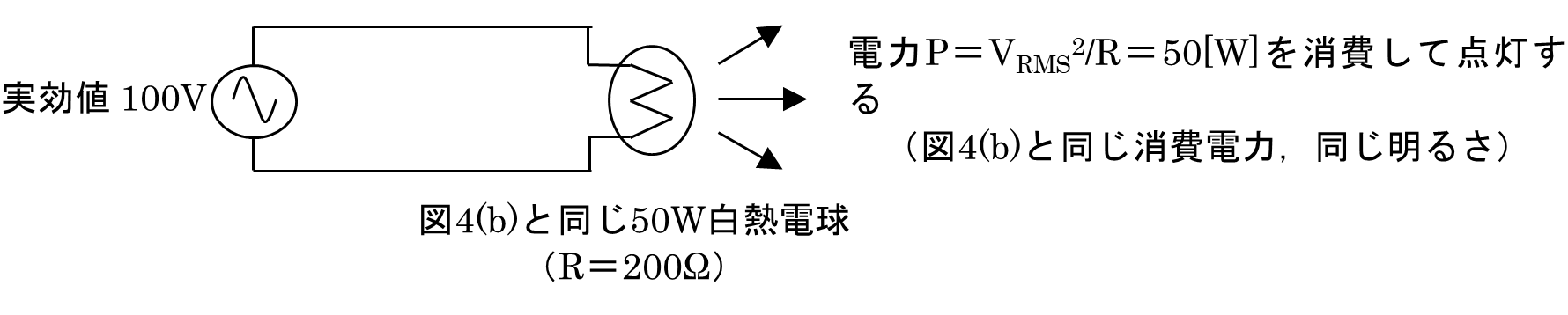
　たとえば，R＝200[Ω]の白熱電球を負荷抵抗として電圧100Vをかければ，電球は

P＝V²/R＝50[W]

の電力を消費して点灯します（図4(b)）．

図4　直流の電圧，電流，電力の関係

(a) 電力は電圧の2乗に比例する

(b) 直流100Vの場合の電力計算の例

●交流における電力とは

 

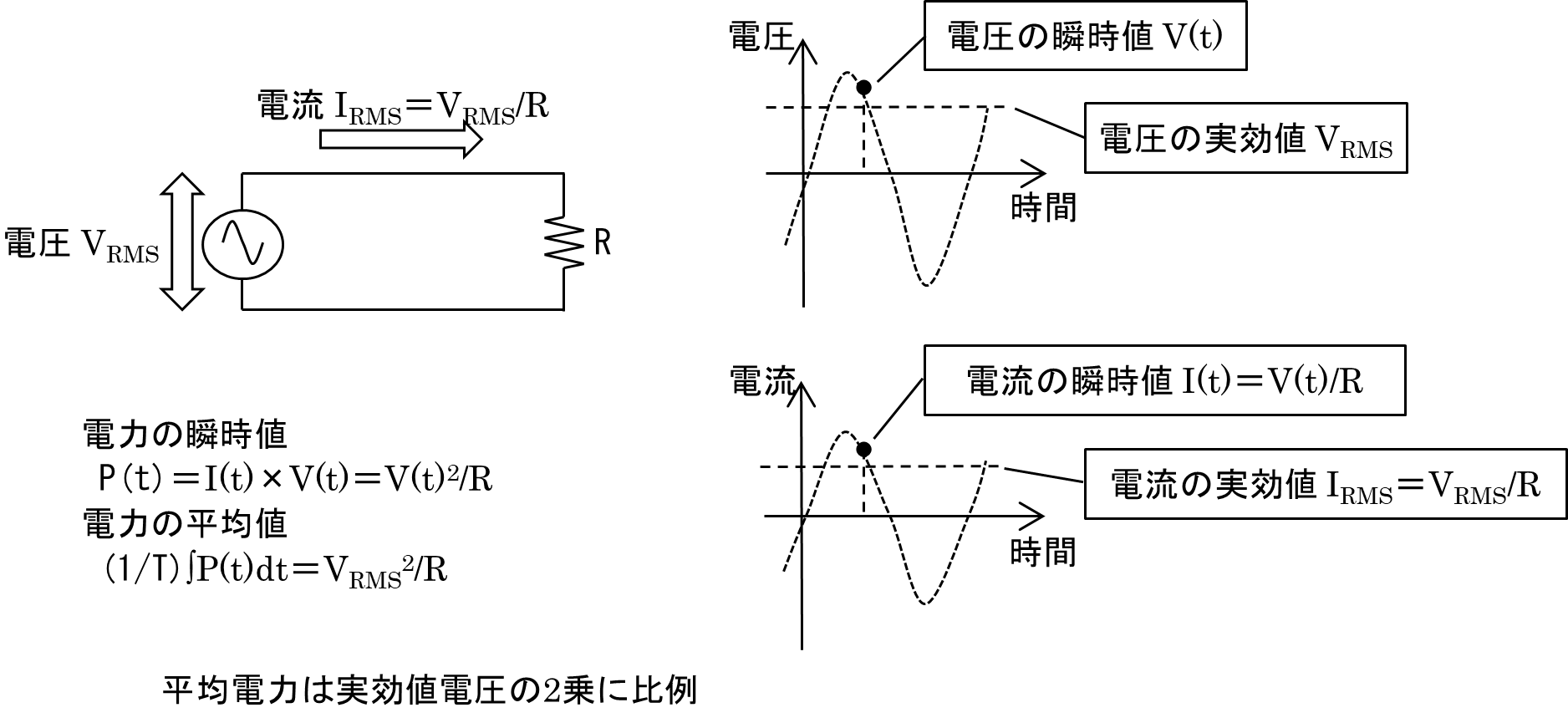
　図5(a)のように負荷抵抗Rに交流電圧V(t)をかけると，各瞬間の電圧V(t)と電流I(t)の間にはオームの法則I(t)＝V(t)/Rが働きます．

　交流では各瞬間の電圧V(t)と電流I(t)の積が，その瞬間の電力P(t)となるので，

P(t)＝I(t)×V(t)＝V(t)²/R　　　　　…④

が電力の瞬時値となります．この瞬間電力を1周期にわたって積分して時間Tで割れば，平均電力を求められます．すなわち，交流電力は

と計算できます．

　ここで1/Rを積分の外に出し，1/Tを中に入れると，

となります．①式の実効値と見比べると，⑤式前半の積分の部分は実効値の2乗であり，

であることが分かります．すなわち，交流の電圧を実効値で表せば，直流の場合の③式と同様に，電圧の2乗を負荷抵抗で割れば交流電力が得られることになります．

図5　交流の電圧，電流，電力の関係

(a) 電力（平均値）は実効値の2乗に比例する

(b) 実効値100Vの場合の電力計算の例

　したがって，解答群のウ「抵抗負荷の場合，実効値100VのAC電源が消費する電力は，100VのDC電源が消費する電力と等しい．」も正しい文章です．

 

●電流の実効値と電力

 

　電圧の実効値と同様に，電流も実効値で表すことができます．実効値I_RMSの式は，

であり，正弦波の交流電流I(t)＝I_msinωtを⑦式に代入すれば，

となります．電流の場合も，実効値I_RMSは尖頭値I_mの約0.71倍となります．

　交流電力の瞬時値を示す④式では，P(t)＝I(t)×V(t)からI(t)を消去して電力を電圧の2乗で表しています．ここで，P(t)＝I(t)×V(t)からV(t)の方を消去すれば，

P(t)＝I(t)²×R　　　　　…⑧

となり，電力を電流の2乗で表すことができて，交流電力は

と表せます．

　交流の電圧，電流を実効値V_RMS，I_RMSで表すと，直流のオームの法則V＝I×R，ワットの法則P＝I×V＝V²/R＝I²×Rなどの式は，そのまま交流に置き換えられます．

V_RMS＝I_RMS×R

P＝I_RMS×V_RMS＝V_RMS²/R＝I_RMS²×R

　ただし，これらが成り立つのは負荷が抵抗の場合に限ります．

　解答群のエ「どのような負荷に対しても，AC電源が負荷で消費する電力の実効値は，電圧の実効値と電流の実効値の積によって求められる．」は，「どのような負荷に対しても」と，「電力の実効値」の2個所に誤りがあります．

　まずお詫びですが，「電力の実効値は」の部分は筆者のスペルミスでした．実効値を用いるのは電圧，電流であり，電力は平均値を用います．

　エは，「どのような負荷に対しても，AC電源が負荷で消費する電力の平均値は，電圧の実効値と電流の実効値の積によって求められる．」とすべき文でした．ただし，「電力の実効値」の部分に違和感を感じてエを選んだ方は，それで正解です．

●負荷が抵抗の場合

 

　エの後半の文章である「AC電源が負荷で消費する電力の平均値は，電圧の実効値と電流の実効値の積によって求められる．」は，式で書けば，

P＝I_RMS×V_RMS　　　　　…⑨

です．

　設問の文でも簡単に説明しているように，これが成り立つには，電圧と電流の位相が一致するという条件が必要であり，それは負荷が抵抗の場合です．

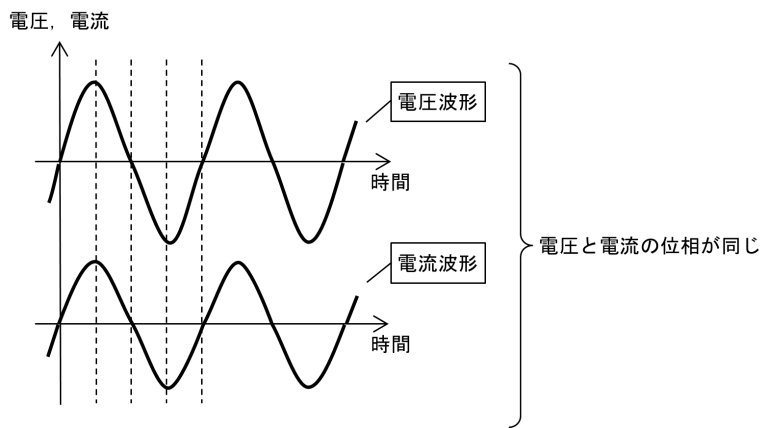
　図6(a)のように，抵抗負荷Rに交流電圧V(t)をかけると交流電流I(t)が流れます．各瞬間のV(t)とI(t)の間にオームの法則V(t)＝I(t)×Rが働き，どの瞬間でも常にV(t)とI(t)が比例しています．したがって，電圧の山と電流の山，電圧の0と電流の0，電圧の谷と電流の谷が一致するので，図6(b)のように電圧と電流は同位相になります．

　各瞬間の電力P(t)はP(t)＝I(t)×V(t)ですが，これは④式のようにV(t)²に比例し，平均電力はV_RMSの2乗から求められます．あるいは，⑧式のようにI (t)²に比例し，平均電力はI_RMSの2乗から求められます．さらに，P＝V_RMS²/RとP＝I_RMS²×Rをかけると，

P²＝I_RMS²×R×V_RMS²/R＝I_RMS²×V_RMS²

なので，

P＝I_RMS×V_RMS

が言えます．

図6　抵抗負荷における電圧と電流の位相

(a) 回路

(b) 電圧と電流の位相

 

●負荷が抵抗でない場合

　回路の負荷としては，抵抗Rの他に，インダクタンスLとキャパシタンスCを考えることができます．そして，LやCに交流電圧をかけた場合，電圧の位相に対して電流の位相が遅れたり進んだりする性質をもちます．

 

●誘導負荷Lの場合

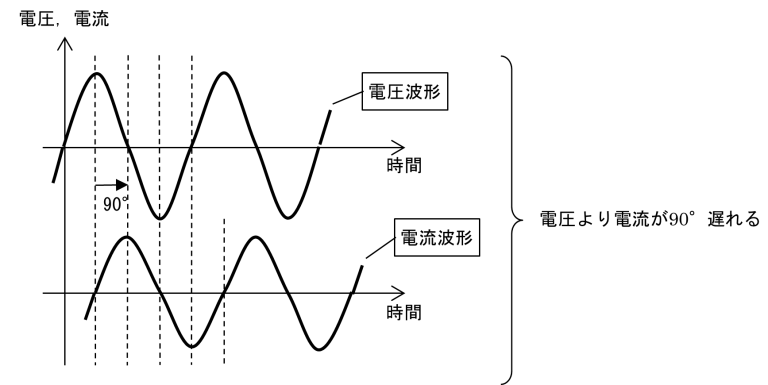
　回路の負荷がインダクタンスLのとき，誘導負荷と呼びます．図7(a)のように，誘導負荷に交流電圧V(t)をかけると交流電流I(t)が流れます．Lには電流の位相を遅れさせる働きがあり，図7(b)のように電圧より電流が90°遅れます．

(a) 回路

 

(b) 電圧と電流の位相

 

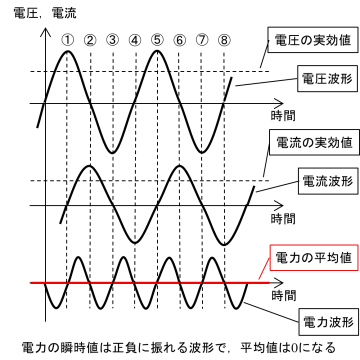
　電圧波形，電流波形と電力の瞬時値P(t)＝I(t)×V(t)の波形の関係を図8に示します．

図8　誘導負荷における電圧，電流と電力の関係

　図8の①，③，⑤，⑦のタイミングは，電流の瞬時値I(t)が0なので，電力の瞬時値P(t)も0になります．また，②，④，⑥，⑧のタイミングは，電圧の瞬時値V(t)が0なので，電力の瞬時値P(t)も0になります．

　さらに，

①と②の間ではV(t)＞0，I(t)＞0なので，P(t)は正の値

②と③の間ではV(t)＜0，I(t)＞0なので，P(t)は負の値

③と④の間ではV(t)＜0，I(t)＜0なので，P(t)は正の値

④と⑤の間ではV(t)＞0，I(t)＜0なので，P(t)は負の値

⑤と⑥の間ではV(t)＞0，I(t)＞0なので，P(t)は正の値

⑥と⑦の間ではV(t)＜0，I(t)＞0なので，P(t)は負の値

⑦と⑧の間ではV(t)＜0，I(t)＜0なので，P(t)は正の値

のように，P(t)は正負に振れる波形であり，平均するとP(t)＝0になります．

　このように，誘導負荷の電力は周期的に正負に変化しており，平均値では0になります．これは，誘導負荷は電力の蓄積と放出を交互に繰り返していて，抵抗とは違って電力を消費しないと考えられます．

　誘導負荷の場合，電圧の実効値V_RMS，電流の実効値I_RMSが0でなくても平均電力Pは0になります．抵抗負荷の⑨式，P＝I_RMS×V_RMS は成り立ちません．

●容量負荷Cの場合

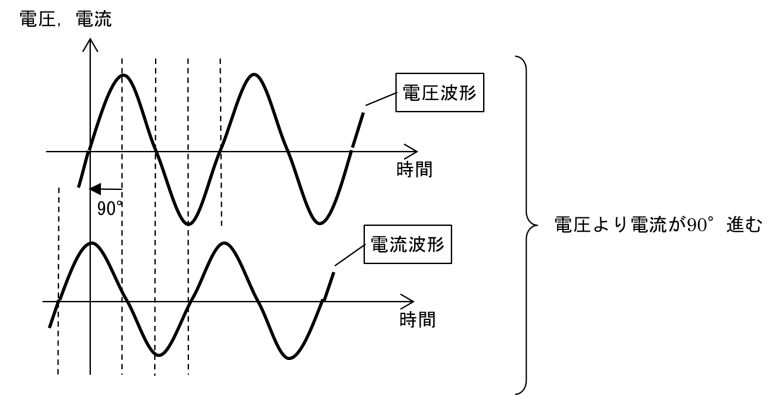
　回路の負荷がキャパシタンスCのとき，容量負荷と呼びます．図9(a)のように，容量負荷に交流電圧V(t)をかけると交流電流I(t)が流れます．Cには電流の位相を進ませる働きがあり，図9(b)のように電圧より電流が90°進みます．

図9　容量負荷における電圧と電流の位相

(a) 回路

(b) 電圧と電流の位相

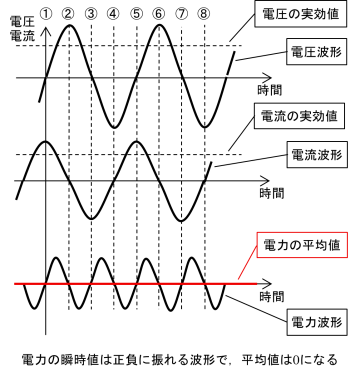
電圧波形，電流波形と電力の瞬時値P(t)＝I(t)×V(t)の波形の関係を図10に示します．

図10　容量負荷における電圧，電流と電力の関係

　誘導負荷と同様に，電力の瞬時値P(t)＝I(t)×V(t)は正負に振れる波形であり，平均するとP(t)＝0になります．容量負荷は電力の蓄積と放出を交互に繰り返していて，抵抗とは違って電力を消費しないと考えられます．

　容量負荷の場合，電圧の実効値V_RMS，電流の実効値I_RMSが0でなくても平均電力Pは0になります．抵抗負荷の⑨式，P＝I_RMS×V_RMS は成り立ちません．

 

　以上のように，電圧の実効値と電流の実効値の積によって電力が求められるのは抵抗負荷の場合だけです．誘導負荷や容量負荷だけの場合は，電圧の実効値や電流の実効値とは関係なく，平均消費電力は0になります．抵抗R，インダクタンスL，キャパシタンスCを組み合わせた負荷の場合，その中のRだけが電力を消費します．LやCには電圧がかかって電流が流れていても，消費電力は0になります．

　したがって，解答群のエ「どのような負荷に対しても，AC電源が負荷で消費する電力の実効値は，電圧の実効値と電流の実効値の積によって求められる．」は誤った記述となっています．

　本問は，「交流電源，直流電源について述べたア～エの文のうち，誤った文を一つ選びなさい．」という問題であり，正解はエになります．