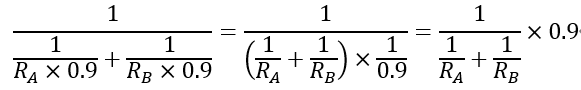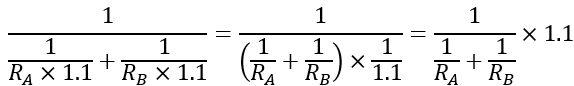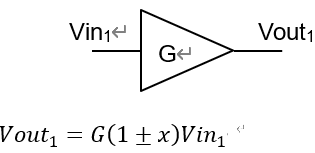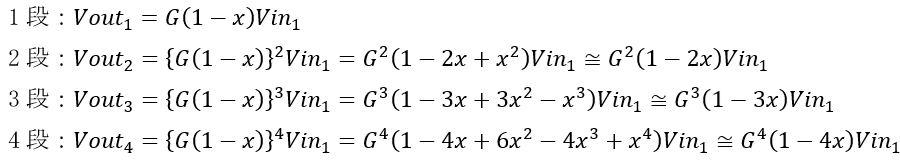トラ技ジュニア検定⑮【正答と解説】複数の抵抗を組み合わせた回路の許容差

トラ技ジュニア No.59(2024秋号)p.36掲載
【トラ技ジュニア検定⑮】「複数の抵抗を組み合わせた回路の許容差」の解答と解説を掲載します. 英語版はコチラ
問題文および図については,誌面にてご確認ください. <宮崎 仁>
[正解]
(イ)
[解説]
単体の抵抗器の精度(許容差)や,複数の抵抗器を組み合わせて作った抵抗回路の精度(許容差)に関する問題です.
●直列接続の許容差を考える
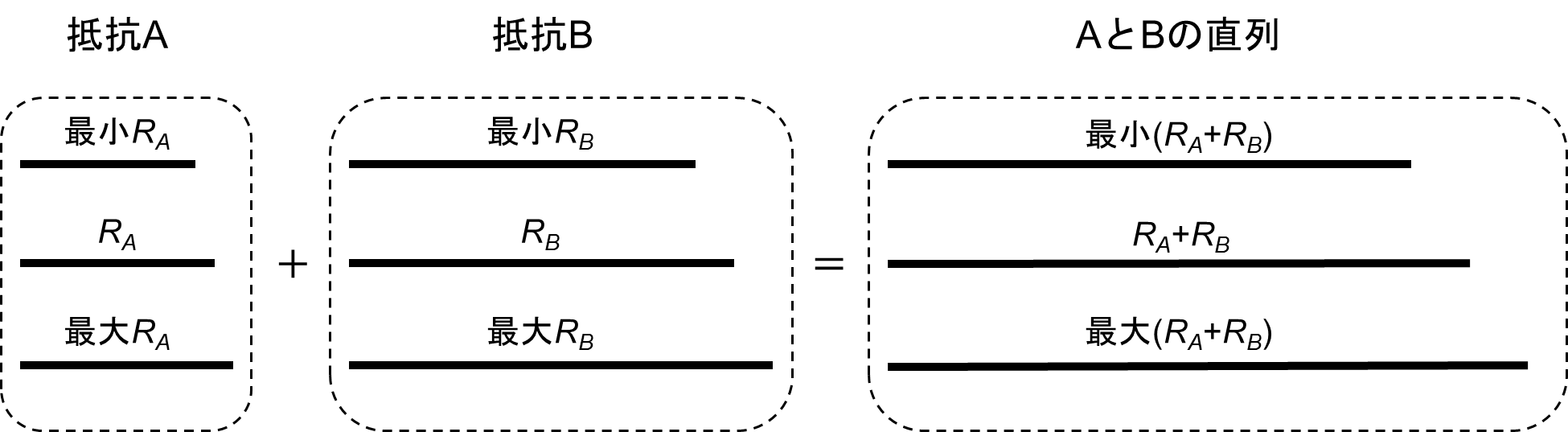
問題の本文で説明しているように,許容差が同じ抵抗を直列接続した場合,合成抵抗の許容差は元の抵抗の許容差と同じになると言えます.例えば,許容差が±10%で公称値がRAの抵抗Aと,同じく許容差が±10%で公称値がRBの抵抗Bを直列接続すると,合成抵抗の公称値はRA+RBで許容差は±10%となります.
これを,図1のように考えてみましょう.
抵抗A,抵抗Bの値はそれぞれ許容差の範囲でバラつきますが,直列接続の合成抵抗の値はそれらの和なので,Aが最小かつBが最小のときA+Bも最小となります.同様に,Aが最大かつBが最大のときA+Bも最大となります.
図1 直列接続の場合の許容差
計算式で考えると,許容差が±10%のとき最小Rは公称値Rの0.9倍,最大Rは公称値Rの1.1倍なので,
RAとRBが最小のとき:
RAとRBが最大のとき:
となり,合成抵抗の最小値は ![]() ,最大値は
,最大値は![]() です.すなわち,合成抵抗の公称値RA+RB に対して最小値は0.9倍,最大値は1.1倍になるので,合成抵抗の許容差 は±10%となります.
です.すなわち,合成抵抗の公称値RA+RB に対して最小値は0.9倍,最大値は1.1倍になるので,合成抵抗の許容差 は±10%となります.
以上より,
① 許容差±10%の抵抗を直列接続した場合,全体の許容差も±10%となる
といえます.
●並列接続の許容差を考える
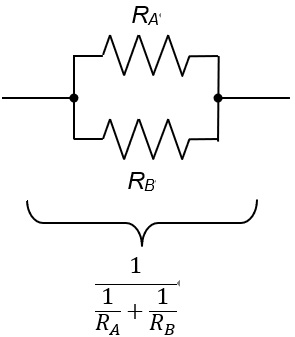
並列接続の場合,図2のように合成抵抗は分数の形になります.
図2 並列接続の合成抵抗
このままではわかりにくいので,まず分母側の
について考えてみましょう.
図3のように,1/RA と 1/RBがともに最小のとき 1/RA+1/RB は最小になり, 1/RAと1/RB がともに最大のとき1/RA+1/RBは最大になります.
図3 並列接続の場合の許容差
ここで,逆数1/Rが最小になるのはRが最大のとき,逆数1/Rが最大になるのはRが最小のときであることに注意すれば,RAとRBがともに最小のとき 1/RA+1/RBは最大になり,RAとRBがともに最大のとき1/RA+1/RBは最小になるといえます.
さらに,並列接続の合成抵抗は 1/RA+1/RBの逆数 ![]() なので,
なので,
といえます.
次に,計算式で考えてみます.
RAとRBが最小のとき:
RAとRBが最大のとき:
となるので,並列接続の合成抵抗の最小値は公称値の0.9倍,並列接続の合成抵抗の最大値は公称値の1.1倍となることがわかります.したがって,直列接続のときと同様に,
④ 許容差±10%の抵抗を並列接続した場合,全体の許容差も±10%となる
といえます.
●選択肢アの検討
ここで,問題文の選択肢アについて検討します.
選択肢アでは,「許容差が±5%の2本の抵抗を並列接続した場合,2本がともに公称値-5%のとき合成抵抗は最大になり,2本がともに公称値+5%のとき合成抵抗は最小になる」と述べています.
「許容差が±5%」で「2本がともに公称値-5%のとき」は,2本がともに最小なので,②より合成抵抗は最小になります.したがって「2本がともに公称値-5%のとき合成抵抗は最大になり」は誤った記述です.
「許容差が±5%」で「2本がともに公称値+5%のとき」は,2本がともに最大なので,③より合成抵抗は最大になります.したがって「2本がともに公称値+5%のとき合成抵抗は最小になり」は誤った記述です.
したがって,問題文の選択肢アは誤った記述です.
●選択肢イの検討
次に,問題文の選択肢イについて検討します.
選択肢イでは,「許容差が±5%の複数の抵抗を直列接続,並列接続して回路を作った場合,その回路の合成抵抗の誤差は±5%の範囲に収まる.」と述べています.
上述の①と④はともに許容差±10%の場合を例に解説していますが,一般に許容差が±x%のときにも成り立ちます.したがって,許容差が±5%の2本の抵抗を直列接続した場合も,許容差が±5%の2本の抵抗を並列接続した場合も,合成抵抗の誤差は±5%に収まります.
さらに,3本以上の抵抗を使った複雑な接続について考えてみます.
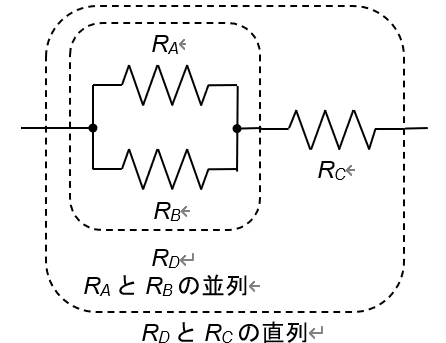
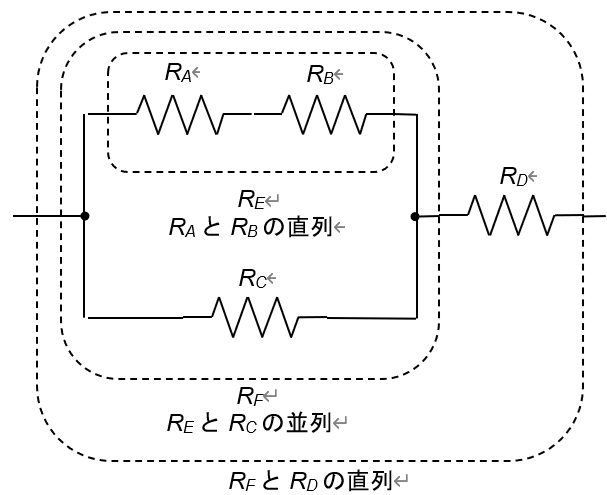
例えば3本の抵抗RA,RB,RCを接続した図4の回路は,まずRAとRBを並列接続してRDを作り,それにRCを直列接続したものと考えられます.同様に,4本の抵抗RA,RB,RC,RDを接続した図5の回路は,まずRAとRBを直列接続してREを作り,それにRCを並列接続してRFを作り,それにRDを直列接続したものと考えられます.
複数の抵抗を組み合わせて作った回路の多くは,このように直列接続と並列接続の組み合わせに分解できます.それぞれの直列接続,並列接続では元の許容差が保たれるので,このような回路の全体でもやはり元の許容差が保たれます.例えば,許容差が±5%の複数の抵抗を直列接続,並列接続して作った回路は,全体としても許容差は±5%であり,合成抵抗の誤差は±5%の範囲に収まります.
したがって,問題文の選択肢イは正しい記述です.
図4 3本の抵抗の直並列接続の例
図5 4本の抵抗の直並列接続の例
なお,複数の抵抗を使った回路の中には,直列接続と並列接続の組み合わせに分解できないものもあります.その場合も,各抵抗の許容差が同じであれば,回路全体の許容差は各抵抗の許容差と同じと考えることができます.
●誤差が蓄積される場合,されない場合
よく「アナログ回路では誤差が蓄積される」といわれます.これは,例えば音声をアナログのテープレコーダで録音し,再生した音声をまたアナログのテープレコーダで録音して,というようにコピーを繰り返すたびに信号が劣化していくことを指しています.
回路の例でいえば,図6のようにゲイン誤差xをもつアナログ増幅回路を,図7のようにN段直列接続する場合を考えます.ここでは,最悪条件として各段の誤差がすべて-xの場合を考えますが,各段の誤差がすべて+xとしても同じです.
図6 ゲイン誤差をもつ増幅回路
図7 ゲイン誤差をもつ増幅回路の直列接続の例
1段目のゲインが![]() ,2段目のゲインも
,2段目のゲインも![]() すると,1段目と2段目の合成ゲインは
すると,1段目と2段目の合成ゲインは ![]() となります.ここで,xは誤差なので1よりも十分小さい(たとえば0.1とか0.01など)と考えられるので,
となります.ここで,xは誤差なので1よりも十分小さい(たとえば0.1とか0.01など)と考えられるので, ![]() の項は
の項は![]() に比べてきわめて小さくなります.
に比べてきわめて小さくなります.
したがって,1段目と2段目の合成ゲインはおよそ ![]() といえます.
といえます.
同様に,1段目から3段目までの合成ゲインはおよそ![]() ,1段目から4段目までの合成ゲインはおよそ
,1段目から4段目までの合成ゲインはおよそ ![]() となり,1段増えるごとに誤差xが蓄積されていくことがわかります.
となり,1段増えるごとに誤差xが蓄積されていくことがわかります.
「アナログ回路では誤差が蓄積される」というのは,このような場合です.
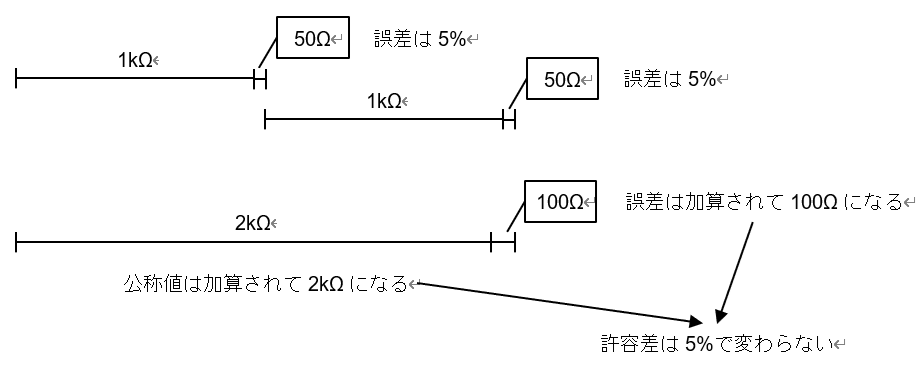
それに対して,抵抗の直並列接続では誤差が蓄積されることはありません.例えば,図8のように公称値が1kΩで誤差がともに+50Ω(1kΩに対して+5%)の抵抗を直列接続すると,誤差は加算されて+100Ωになりますが,公称値の部分も加算されて2kΩになるので,公称値と誤差の比は変わりません.
図8 直列接続では公称値も誤差も加算される
●選択肢ウの検討
問題文の選択肢ウについて検討します.
選択肢ウでは,「公称値が1kΩで,許容差が±5%の抵抗を何本も直列接続していくと,誤差が蓄積することによって合成抵抗の誤差が±5%より大きくなってしまうことがある.」と述べています.
これまで見てきたように,許容差が同じ抵抗を直列接続した場合,合成抵抗の許容差は元の抵抗の許容差と変わりません.1kΩ,±5%の抵抗をN本直列接続した場合,合成抵抗の公称値はNkΩとなり,許容差は±5%のままです.
したがって,問題文の選択肢ウは誤った記述です.
●値のバラつきと許容差を考える
問題文でも説明しているように,抵抗器の実際の抵抗値は何らかの誤差をもっており,公称値ぴったりではなく,バラつきをもっています.バラつきの範囲の最小から最大までが許容差です.したがって,例えば公称値が1kΩで許容差が±1%の抵抗であれば,実際の抵抗値は990Ω(1kΩ-1%)から1010Ω(1kΩ+1%)の範囲のあらゆる値を取る可能性があります.
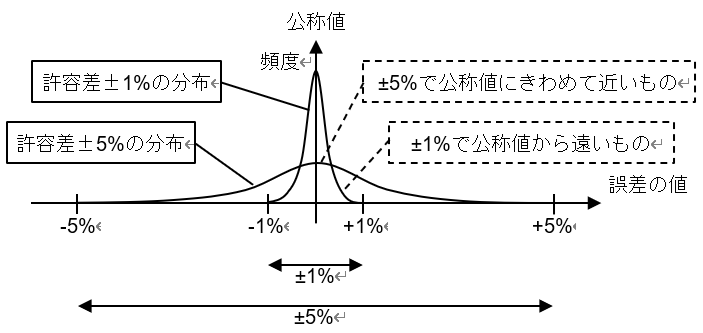
このバラつきは,抵抗器の製造工程での物理的な変動から生じるものです.一般には,図9のように範囲の中央付近の頻度が高くなり,範囲の両端に近づくほど頻度が低くなります.このような分布の中で,最もきれいな形のものが正規分布です.実際の抵抗器の場合は正規分布にはなりませんが,似たような分布になることが期待されます.
図9 実際の抵抗器の抵抗値の分布の例
ここで,許容差±1%と許容差±5%の分布を比較すると,±1%の方が公称値に近いものが多く,±5%の方が公称値から遠いものが多いことが分かります.しかし,±5%でも公称値にきわめて近いものがあり,±1%でそれより公称値から遠いものもあります.すなわち,±1%の抵抗が常に±5%の抵抗より公称値に近いとは言えません.
●選択肢エの検討
問題文の選択肢エについて検討します.選択肢エでは,「公称値が1kΩで,許容差±1%の抵抗と±5%の抵抗の実際の値を比較すると,±1%の抵抗の方が常に1kΩに近い値になっている.」と述べています.
上述の説明のように,±5%の抵抗でもきわめて1kΩに近い値のものがありますし,±1%でもそれより1kΩから遠いものもあります.±1%の抵抗の方が常に1kΩに近い値ということはありません.
したがって,問題文の選択肢エは誤った記述です.
以上をまとめると,選択肢のうちア,ウ,エは誤った記述,イは正しい記述であり,本問の正解はイになります.